Navigation at sea is easy nowadays. We have electronic charts and GPS. The chart provides a map and the GPS tells us where we are. Easy.

But what do you do when you are chatting with your friends in the cockpit and you want a rough estimate of how far away from something you are? Say there is a headland and you want to be 3 miles off because of the overfalls (turbulent water caused by strong tides and such).

There are simple methods. If you can see people walking on the headland you are likely within a mile – too close! The rough answer is that you need to be at least three times further off.

A more sophisticated way to know rests on the rate the earth curves away from us. With an eye height of 3 metres above the sea, your furthest horizon is some 3.6 miles away. Anything at sea level further in the distance has dipped away below the horizon because of the curvature of the earth. This phenomenon is known as “dipping height” and you can calculate it for various heights using a table in a nautical almanac. This means that if you, standing in the cockpit of your boat, can see waves breaking on the beach you are too close. It’s similar with a ship. If you can’t see its bow wave or its waterline, the ship is over three miles away. So, to be more than three miles off the headland, we need to be out of range of the surf.

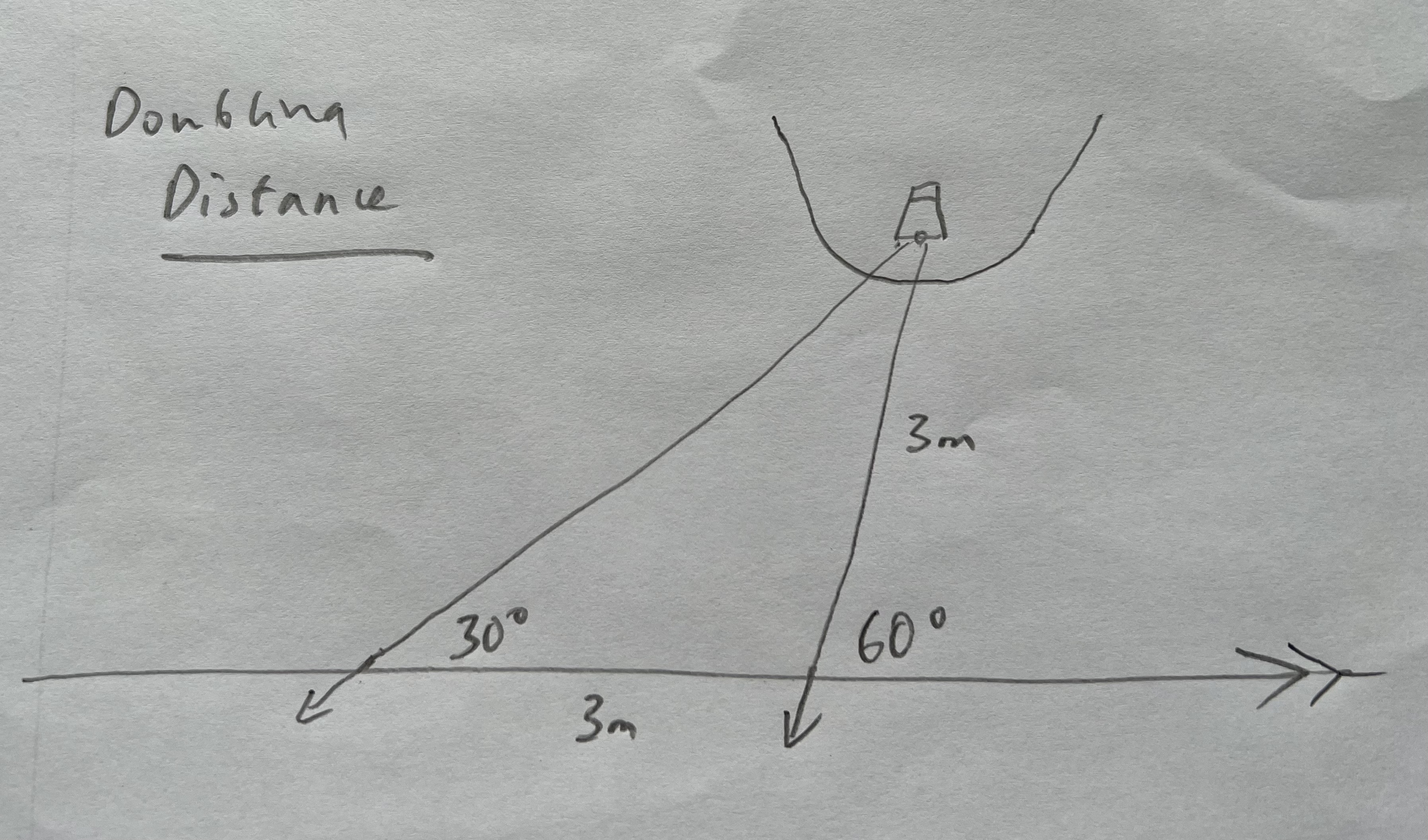
Doubling distance is a rule of thumb that is based on triangles. Say you are passing the headland going east. If you look at a tower on the headland and it is an angle of 30 degrees off the bow then you make a note of the time and speed you are going and wait until the tower is 60 degrees off the bow. Using your speed you can work out how far you have travelled in that time, factoring in any tidal effect if needed. At the point the angle has doubled the distance from the tower is the same as the distance you have travelled. This is because you have now made an equal sided “isosceles” triangle. If it took you longer than three miles to double the angle, you are far enough off.

None of this trigonometry and maths stuff is strictly necessary and I generally find there’s a part of me that rebels when I try it out. I’ve learnt though, that I enjoy the challenge. There’s a satisfaction in knowing that you can get by on your own wits without modern technology if you have to.

I’ve also noticed that it provides a nice balance to what is otherwise a deeply practical and immersive experience. You can just sat nav your way through but somehow adding a degree of observation and knowledge to the process makes the whole experience richer.

I wonder how true that is of everyday life also. How much information is there around us that we just miss because we’ve found ways of getting by without it?

Footnote:

All these miles are nautical miles by the way, slightly bigger than land miles. This is annoying but sea miles are themselves based on an angle, equalling one minute of latitude. On a spherical planet this makes chart work easy as every degree you travel North or South is 60 miles. They are 1852 metres or 1.15 land miles.